14. Indeksid

Indeks on andmebaasi juhtimissüsteemi funktsionaalne instrument, mis võimaldab muuta kiiremaks andmete (kirjete) pärimise andmebaasist – leida indeksist kiiresti võtme väärtuse järgi kirje aadressi ja selle aadressi alusel pöörduda juba kirje enese poole. Indeksite olemust võib kirjeldada ka teisiti. Indeksid võimaldavad kirjeldada andmete juurde "otsetee". Kui sellised "otseteed" puuduksid, peaksime me mingite meile vajalike andmete leidmiseks vaatama läbi järjest kõik tabeli read tabeli algusest lõpuni. Siit võib teha täiesti selge järelduse - indeksid muudavad andmete otsimise ja leidmise andmebaasi tabelitest oluliselt kiiremaks.

Indeksite sisemine struktuur võib olla väga erinev. Andmebaasisüsteemide arengu käigus on mõeldud välja väga erineva sisemise struktuuriga indekseid. Erinevate andmebaasisüsteemide tootjate vahelises võitluses on indeksid väga tähtsal kohal. See, kui kiiresti suudetakse anded andmebaasist üles leida ja kui vähe andmete otsingule kulutatakse protsessori aega, on väga oluline, kui arvestada andmebaasiserverite piiratud ressurssi.

Kuidas indeks toimib ja milline on ta sisemiselt? Vaatamata erinevate indeksite erinevale sisemisele struktuurile ei ole indeksite toimimise loogikat väga raske selgitada. Esimene, millest tuleb aru saada, on see, et indeksid ei kiirenda otsingut mistahes tingimuse alusel vaid ainult nende tingimuste järgi otsingut, mille otsingu väljad on indekseeritud.

Indeks on struktuuri poolest tabel, millele on vähemalt kaks veergu. Erineva keerukusega indeksil võib muidugi olla veerge ka rohkem, aga enamuses piisab kahest veerust. Siin ei tohi muidugi seda "tabelit" segi ajada andmebaasitabeliga. Indeksil on lihtsalt tabeli struktuur aga vaatamata sellele ei ole ta "andmebaasi tabel" vaid siiski ainult indeks. Indeks saab eksisteerida ainult seose mingi tabeliga ja selle tabeli hävitamisel andmebaasist kaob ka indeks. Tabeli hävitamisel andmebaasist (DROP TABLE) kaovad andmebaasist ka kõik selle tabeliga seotud (selle tabeli jaoks loodud) indeksid.

Indeksi loomiseks kirjeldatakse indeksi võtme struktuur ja antakse indeksile unikaalne nimi. Loomulikult määratakse ka andme-tabel, millele indeks luuakse. Selle nime järgi on võimalik indeksit hävitada ka ilma hävitamata seda tabelit, millega see indeks on seotud. Indeksite võtme struktuuri ei saa muuta. Kui tekkib vajadus indeksi võtme struktuuri muutmiseks tuleb indeks hävitada ja luua kas sama või mingi muu nimega uus indeks. Oluline on mõelda indeksi uue nime all loomisel seda, et ega me juhuslikult pole kasutanud seda indeksi nime mingid SQL-kompilaatorile antud juhises kasutada päringus just seda indeksit

Millised on siis need indeksi veerud ja kuidas neid väärtustatakse? Esimene veerg sisaldab otsingu võtit ja teine sellele võtmele vastava kirje aadressi tabelis. Uue kirje kirjutamisel andme-tabelisse kirjutatakse rida ka igasse indeksisse, mis on selle tabeliga seotud. Igasse indeksisse rea lisamisel moodustatakse tabelisse lisatud kirje väärtustest indeksi võtme kirjelduse alusel võtme väärtus, loetakse kirje aadress ja kirjutatakse need väärtused indeksisse - võtme väärtus esimesse veergu ja aadress teise veergu.

Kui kirje kustutatakse andme-tabelist, siis kustutatakse kõik selle kirjega seotud read ka kõikidest selle tabeliga seotud indeksitest. Kui kirjes muudetakse nende veergude väärtused, mis on kasutatud mõne indeksi võtme moodustamiseks, siis nendes indeksites kustutatakse vana indeksi kirje ja kirjutatakse uus indeksi kirje. Tegelikkuses on tihti küll nii, et kõikidesse indeksitesse, sõltuvalt indeksi tüübist, ei kirjutata rida iga andme-tabeli kirje kohta. On olemas indekseid, kus kirjeid grupeeritakse ja indeksisse kirjutatakse üks rida iga kirjete grupi kohta. Sellistes indeksites ei viita aadress-väli konkreetsele kirjele vaid kirjete grupi esimesele kirjele.

Indeksi võtmete väärtused on mingil moel järjestatud võtmete väärtuse järgi. Miks ma ütlen "mingil moel"? Nagu te hiljem näete, on indeksis võtme "järjestusi" väga erinevaid ja kõik ei ole sugugi nn. "puhtad järjestused". Lisaks tavalistele sorteeritud jadadele kasutatakse Indeksi võtmete "järjestamiseks" erinevaid hierarhilisi struktuure, kus indeksi võtmete järjestus ei ole pidev terve indeksi ulatuses vaid ainult erinevate hierarhia tasemete piires. On muidugi ka üks indeksi tüüp, "paisk-indeks" (hash table), kus indeksi väärtused ei ole üldse sorteeritud, vaid esmapilgul täiesti segamini. Siiski on selle segaduse aluseks alati täiesti konkreetne funktsioon, mille alusel indeksi väärtusi indeksisse paigutatakse ja neid sealt hiljem otsitakse. Kui väärtuste tabelisse paigutamisel ja nende lugemisel (asukoha otsimisel võtme väärtuse järgi) kasutatakse sama funktsiooni, siis töötab ju see asi päris hästi. Kui me otsimisel teeme võtme väärtuse järgi sama arvutuse, kui me tegime seda võtme väärtuse tabelisse paigutamisel, siis me saame ju kontrollida, kas indeksi selles kohas, kuhu me eeldatavasti kunagi paigutasime võtme väärtuse on tõepoolest see võtme väärtus olemas. Kui on, siis loeme indeksi võtme väärtuse kirjest andme-tabeli kirje aadressi ja seejärel selle aadressiga määratud andme-tabeli kohast andmekirje enese. Kui me indeksist võtmeväärtust ei leia, siis järelikult sellise võtme väärtusega kirje puudub ka andme-tabelis.

Käesolevas jaotises esitatakse indeksite klassifikatsioon ja kirjeldatakse peamiste indeksi tüüpide sisemist struktuuri ning toimimist.

14.1. Raamatukogu näide

Heaks näiteks indeksite olulisusest on käsitsi-otsingu süsteemil toimiv raamatukogu. Veel üsna hiljaaegu ei saanud raamatukogudes, kus tänapäeval on enamuses juba kasutusel arvutipõhised raamatu otsingu süsteemid, hakkama ilma puukastide ja kartoteegi kaartidega indeksiteta. Vaatamata arvutite levikule leidub tänapäevalgi veel palju väikesied raamatulogusid, kus kartoteegi kastidel põhinev otsingusüsteem on veel kasutuses.

Raamatukogu indeksiteks on kataloogid. Kujutage ette raamatukogu, kus oleksid riiulitel raamatud ja nende kohta ei oleks olemas ühtegi otsingu kataloogi. Kui raamatud oleksid riiulitel sorteerimata (täiesti suvalises – näiteks raamatukokku saabumise järjekorras), siis tuleks meil halvimal juhul mingi konkreetse raamatu leidmiseks läbi vaadata kõik raamatukogus olevad raamatud. Seda juhul, kui ta juhtub olema viimane raamat selles jadas. Igal juhul tuleb läbi vaadata kõik raamatud tõdemaks, et meie poolt otsitud raamatut selles raamatukogus ei ole.

Vaatame, kuidas raamatukogu indeksite süsteem töötab. Eeldame, et meil on raamatukogu, kus toimib veel kartoteegikaartidel põhinev indeks.

14.1.1. Raamatukogu käsitlemine registrite abil

Tavaliselt on raamatukogudes olemas nimede tähestikuline register, kus raamatud on sorteeritud autorite nimede ja pealkirjade järgi ning aineregister, kus raamatud on grupeeritud teemade järgi ja teema sees ilmumise aja järgi. Lisaks sellele on suuremates raamatukogudes, kus raamatute arv on suurem, olemas veel erinevates keeltes välja antud raamatute registrid. Eraldi peetakse perioodika ja entsüklopeediliste teoste registreid. Viimast siiski peamiselt suuremates raamatukogudes. Iga selline register on erineva võtme struktuuriga indeks.

Kõik need registrid koosnevad kaartidest (sama indeksi kirjega). Igas sellise registri kaardi peal (olenemata registrist) on olemas eraldi kaardi ülemise serva peal esile tõstetud registri võtme väärtus, kõik raamatu andmed ja lisaks sellele veel raamatu aadress raamatukogus. See viimane näitab, millises osakonnas, millises sektsioonis, millisel riiulil, mitmes köide antud raamat on. Kogu ülejäänud tehnika seisneb kaartide sorteerimises – kaardid on sorteeritud mingis konkreetses järjekorras so. registri võtme alusel, jagatud sorteerimise järjekorras erinevatesse kastidesse, kastid on tähistatud selle võtme vahemikuga, millised kaardid konkreetsesse karpi kuuluvad ja sahtli sees on “kaardipaki” vahele teatud arvu kaartide tagant pandud viidalipikud, mis lubavad “kaardipakis” kiiremini õiget kohta leida. Nüüd on raamatu leidmiseks vaja:

1. teada kas või mingeid andmeid selle raamatu kohta
2. valida välja register, mille võtme me nendest andmetest saame koostada
3. koostada võti
4. leida kartoteegi kast, milles olevate kaartide võtmete vahemiku koostatud võti kuulub
5. leida katist vahe-lipikute abil see sektsioon, kuhu koostatud võti kuulub
6. vaadata selle sektsiooni kaardid järjest läbi ja leida vajalik kaart; kui seda sal pole, siis pole raamatukogus suure tõenäosusega ka seda raamatut; või üritada otsingut korrata mõnes teises registris.

Kui kaart on leitud loetakse kaardi pealt raamatu asukoha aadress. see on piisav raamatu leidmiseks raamatukogu riiulitelt; raamat võib muidugi olla välja antud, kuid see ei tähenda, et seda raamatukogus pole - keegi on sellele raamatule lihtsale exclusive (X-lock) luku pannud. Seda seniks, kuni ta on raamatu läbi lugenud ja raamatukokku tagasi toonud.

Nii piisab raamatu leidmiseks õige kaarti leidmisest (mida on ka füüsiliselt tunduvalt lihtsam teha, kui vahetu raamatu otsimine) ja kaardi pealt saame aadressi, kuhu peame jalutama, et riiulist raamat võtta. Lisaks sellele ei saa raamatuid järjestada korraga mitmes järjestuses. Raamatud saavad olla järjestatud ainult ühes järjestuses. Samas raamatukogus saab aga olla mitu erinevat registrit, kus registri võti on erineva struktuuriga ja võimaldab meil raamatuid otsida isegi siis, kui me teame selle raamatu kohta väga vähe.

Raamatu otsimiseks tähestikulises registris peame me teadma kas autori nime või raamtu pealkirja. Selles registris on võtme väärtusteks autorite nimed ja raamatute pealkirjad. Kui raamatul on kaks autorit, siis on tema kohta selles registris kolm kaarti - raamtu nime järgi üks kaart ja mõlema autori järgi üks kaart. Nii võime me otsida siin registris üks kõik millise järgi nendest.

Temaatilises registris otsimiseks peame me teadma oysitava raamatu temaatilist klassifikatsiooni. Selle täpsustamisel aitab meid temaatiline register ise. Me peame mõtlema välja kõige laiema klassifikaatori, mida me teame ja täpsustame seda temaatilises registris. Näiteks kui me tahame otsida, milliseid andmete modelleerimise kohta kirjutatud raamatuid on ramatukogus hakkame me pihta teemast "infotöötlus". Selle märksõna alt leiame infotöötluse sisemise klassifikatsiooni, kust valime "andmebaasid" ja selle sisemisest klassifikatsioonist teema "andmete modelleerimine". See teema on ilmselt juba nii täpne, et siin viidatakse sellel kartoteegi kastile (anatakse selle number), kust leiate andmete modellerimise raamatuid kirjeldavad kartoteegi kaardid. Need raamatud on selles kastis sorteeritud ilmumisaasta järgi sorteerituna. Nüüd võime me vaadata läbi kogu lloendi kas algusest lõpuni või lõpiust alguseni. Viimasel juhul näeme me esimesena uusi raamatuid. Võib oletada, et just sedasi leiame me endale vajaliku raamatu kõige suurema tõenäosusega.

14.1.2. Raamatukogu registrite uuendamine

Kui raamatukogusse tuleb uus raamat (või mitu sama sugust raamatut), siis koos raamatute hoidla riiulisse paigutamisega, tuleb raamatu kaart lisada kõikidesse registritesse ja mis olulisim – õigesse kohta. Kui seda mitte teha (või teha mitte korrektselt – panna kaart valesse kohta), siis raamatut raamatukogu hoidlas just kui polekski, sest keegi ei oska seda kaarti valest kohast otsida.

Kui raamatukogu saab juurde mõne juba olemasoleva raamatu uue eksemplari, siis võib selle panna riiulisse ilma registreid muutmata. Eelduseks on ainult see, et eksemplar pannakse teiste analoogiliste juurde.

Kui raamatu viimane eksemplar raamatukogust kaob või lihtsalt kasutamiskõlbmatuks muutub (närustub), siis tuleb antud raamatu kaardid kõrvaldada kõikidest registritest.

Märkate sarnasust sellega, mida me enne rääkisime seoses andmebaasi indeksitega? Sarnasus on ilmne.

Tahaks tuua veel ühe viite kirjeldatud sarnasusele andmebaasi indeksitega. On võimalik, et ka andmebaasi indeksid riknevad, st. et indeksi kirjed satuvad vakesse kohta ja indeksi võtmeväärtuste järjestus saab rikutud. Sellisel juhul ei ole võimalik ka selle indeksiga seotud andmebaasi tabelist enam midagi õiget leida. Andmebaasis on muidugi asi lihtsam kui kartoteegis. Riknenud indeksi saab lasta andmebaasi mootoril lihtsalt uuesti üles ehitada. Kui indeksi uuendamise mehhanism konkreetses andmebaasisüsteemis puudub piisab sellest, kui indeks hävitada ja seejärel uuesti luua.

14.2. Erinevat tüüpi indeksid

Indekseid võib jagada:

• ühe-tasemelisteks ja mitme-tasemelisteks indeksiteks
• hõredateks ja tihedateks indeksiteks
• järjestatud ja järjestamata indeksiteks

Kõik need omadused võivad omavahel kombineeruda. Muidugi ei saa omavahel kombineeruda ühe ja mitme tasemelisus, hõredus ja tihedus, järjestatus ja järjestamatus, kuid peaaegu kõik ülejäänud kombinatsioonid on lubatud. Indeksi omaduste kombinatsioone piiravad järgmised kitsendused:

• hõre indeks on alati järjestatud, samas võib see olla ühe- või mitme-tasemeline
• tihe indeks võib olla nii järjestatud kui järjestamata, samas võib see olla ka ühe- või mitme-tasemeline
• järjestamata indeks on alati tihe

Mida see kõik tähendab, seda mõistate siis, kui tutvute järgnevates jaotistes kirjeldatuga.

14.2.1. Ühe-tasemelised järjestatud indeksid

Ühe-tasemeliste indeksite idee on analoogiline tavaliste teaduslike ja tehniliste raamatute indeksitega, mis on raamatu lõpus ja kus märksõnade juures on kirjeldatud kus leheküljel see sõna esineb (mitte segi ajada sisukorraga). Kui meil on vaja leida raamatust meie poolt soovitud mõiste kohta informatsiooni, siis on väga lihtne otsida see märksõna üles raamatu indeksist, vaadata sealt nende lehekülgede numbrid, kus seda sõna on kasutatud ja siis vaadata juba otse nendelt lehekülgedelt. Vastasel korral (kui indeks puuduks) tuleks selle märksõna kohta kirjutatu leidmiseks lehitseda läbi kogu raamat.

Ühe tasemeline järjestatud indeks moodustatakse tavaliselt andme-tabeli ühe välja järgi. Seda võib siiski moodustada ka mitme välja järgi. Sellisel juhul moodustatakse indeksi võti sidurdades nende väljade väärtused kokku. Kokku sidurdamine peab kõikides kirjete indekseerimisel toimuma alati samas järjestuses. Indeksi moodustamiseks tehakse kahe veeruline tabel (indeks) kus esimesse veergu kirjutatakse võtmete väärtused ja teise veergu, iga võtmeväärtuse järele, kirjutatakse nende andmebaasi lehekülgede või kirjete aadresside loend või ka ainult üks aadress (see sõltub konkreetsest andmebaasi indeksi realisatsioonist), millel leidub kirjeid, mille võtme-veergude väärtus on selline nagu indeksi kirjes. Kuna tegemist on sorteeritud loendiga, siis on seal väga lihtne otsida kahend-otsinguga (kahend-otsing10⁹ indeksi kirje hulgas koondub 30-ne korraga).

Andmebaasides kasutatakse mitmeid erinevaid ühe-tasemelisi järjestik-indekseid. Järgnevalt vaatamegi neid.

14.2.1.1. Primaarindeks (Primary Index)

Primaarindeks on fikseeritud pikkusega kirjete loend, millest igal on kaks veergu. Esimeses veerus on võtme väärtus ja teises selle andmebaasi lehekülje aadress kus paikneb antud võtme väärtusele vastav kirje. Indeks vastab tabeli primaarvõtmele (Primary Key) ja indeksi võtme väärtus saadakse tabeli primaarvõtmest.

Andmebaasi lehekülg on ühe andmebaasi jaoks fikseeritud suurusega blokk, kuhu iga tabeli puhul on salvestatud konkreetse tabeli kirje pikkusest sõltuv arv kirjeid. Andmebaasi lehekülg on korraga andmebaasist leotava ja sinna salvestatav andmete kogus. Seega paljudel juhtudel polegi mõtet indeksit täpsemalt adresseerida, kui lehekülje täpsusega. Kui lehekülg on määratud, siis loetakse korraga sisse ja sealt otsitakse õige kirje üles järjestikotsinguga. Kuna leheküljel olevate kirjete arv pole suur ja mäluoperatsioonid on kiired, siis ei võta see jadaotsing palju aega.

Lehekülge adresseerivates indeksites ei kuulu indeksisse üldsegi kõikide kirjete võtme väärtused, vaid ainult lehekülgede esimeste kirjete võtmeväärtused. Sellist indeksit, kus kõigi kirjete võtmete väärtustega rida ei ole indeksis, vaid ainult osade kirjete (lehekülgede esimeste kirjete) võtmeväärtused on indeksis olemas nimetatakse hõredateks indeksiteks.

Siit võib siis kohe järeldada, et tihedateks indeksiteks nimetatakse selliseid indekseid, kui andmetabeli kõikide kirjete võtmeväärtused on olemas ka indeksid. See tähendab siis seda, et igale andme-tabeli kirjele vastab üks indeksi kirje.

Indeksist otsimisel leitakse järjestikuste indeks-kirjete paar, mille vahele otsitava kirje võtme väärtus jääb (esimese indeksi kirje võtme väärtus kaasa arvatud, teise indeksi kirjeväärtus välja arvatud) ja otsitakse siis kirjet järjestikotsinguga leitud indeks-kirjete paari esimese kirje poolt osutatavast andmetabeli leheküljelt. Indeksist otsitakse võtme väärtust kahendotsinguga.

Oletame, et meil on ploki pikkuseks 10 kirjet ja tabelis on 1 000 000 000 kirjet. Primaarindeksis on sellisel juhul 100 000 000 rida. Ploki leidmine indeksist kahendotsingu abil koondub 27 korraga. Kui kirje juhtub olema ploki viimane kirje, siis peame tegema mälus veel 9 lugemist (seda et ta esimene kirje ei ole me juba teame, kuna indeksi võti ei langenud tema võtme väärtusega kokku). Seega saame me kirje halvimal juhul 36 lugemisega, millest üheksa toimub mälus ja ei võta praktiliselt üldse aega. Kuna aga kirjed on blokis keskmiselt neljandad või viiendad, siis saame tulemuse keskmiselt 31-32 lugemisega. See on tegelikult sama kiire, kuna nagu öeldud, mälus kirjete läbi vaatamine on praktiliselt momentaalne.

Täpselt sama arvu lugemistega saame me teada, et otsitavat kirjet tabelis ei ole (kui seda seal tõepoolest pole).

Vaatame nüüd, kuidas üks primaarindeks välja näeb. Selleks teeme joonise, kus on näha nii andmetabel kui ka indeks:

Primaarindeksi rakendamisel on mitu probleemi. Primaarse indeksi probleemiks on indeksisse uute ridade lisamine ja sealt ridade kustutamine. Uue kirje lisamisel tabelisse võib tekkida vajadus kirje lisamiseks indeksisse. Seda juhul, kui lisatav kirje sattub andmetabelis uue bloki esimeseks kirjeks. Sellisel juhul tuleb lisada kirje ka indeksisse vajalikule positsioonile kirjete järjestuses (vastavalt võtme väärtusele). See võib tingida vajaduse taha poole jäävaid kirjeid edasi nihutada, et teha uuele indeksi kirjele kohta. Kirje kustutamisel võib tekkida vajadus kas indeksi uuendamiseks (kui kustutatakse bloki esimene kirje – ankur-kirje) või indeksi rea kustutamiseks (kui kustutati viimane kirje plokist). Esimesel juhul tuleb uuendada ainult võtme väärtus. Teisel juhul peame me indeksist kustutama kirje ja “tõmbama kokku) taha poole jäävaid indeksi kirjeid.

Primaarindeks on hõre, järjestatud ja ühe-tasemeline indeks. Hõre indeks, nagu ees poole kirjeldatud, tähendab seda, et kõigi andmetabeli kirjete võtmeväärtusi ei ole indeksis. Järjestatud indeks tähendab seda, et indeksi kirjed on sorteeritud võtmeväärtuse kasvamise või kahanemise (sellel pole tähtsus kummas järjestuses) järjestuses. Ühe tasemeline indeks tähendab seda, et indeksi kõik kirjed paiknevad samal tasemel st. ühtses jadas.

14.2.1.2. Kobarindeks (Cluster Index)

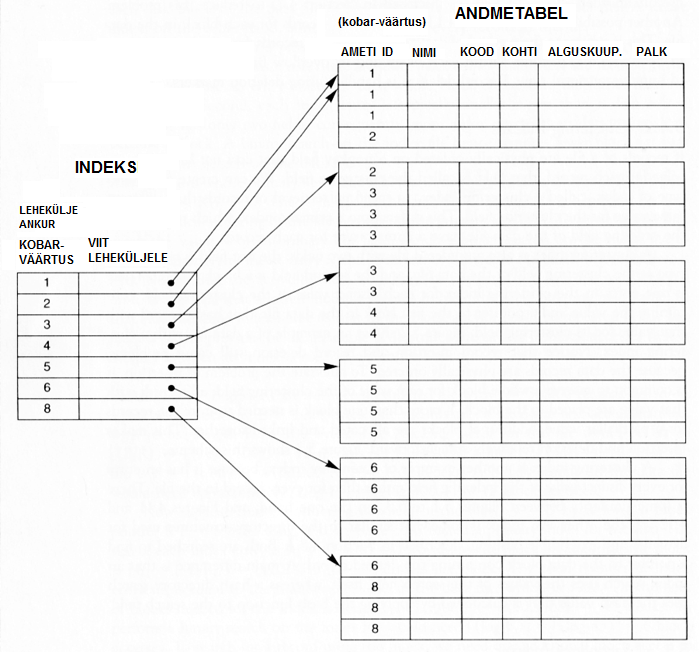
Kui tabeli kirjeid on järjestatud mingi tunnuse (tabeli veeru) alusel, mis ei ole unikaalne (non-distinct), siis sellist väärtust nimetatakse kobar-väärtuseks (cluster value/field). Sellele väärtusele ehitatud indeksit nimetatakse kobar-indeksiks. Kobar indeksi kirjel on kaks veergu – võtme väärtuse veerg ja lehekülje alguse viida veerg. Kobar-indeksis leidub rida andmetabeli iga erineva kobar-väärtuse kohta (indeks-kirje esimeses veerus). Seejuures viitab teine veerg tabeli sellele leheküljele , milles on esimene vastava võtmeväärtusega kirje. Kõik tabeli sama võtme väärtusega kirjed ei pruugi olla samal tabeli leheküljel. Küll on nad aga järjestikustes tabeli plokkides ja paiknevad järjest.

Kobar-indeksist otsimisel otsitakse indeksist ette antud võtme väärtuse järgi üles indeksi rida ja võetakse sealt lehekülje aadress. Seejärel pöördutakse aadressi järgi andmetabeli lehekülje poole ja loetakse sealt kirjeid järjest seni, kuni leitakse kirje mille indekseeritud välja väärtus on võrdne otsitava võtme väärtusega. Nüüd loetakse kirjeid, seni, kuni indekseeritud välja väärtus (kobar-väärtus) jääb võrdseks ette antud otsingu võtme väärtusega või kuni tabeli lõppemiseni (kui etteantu võtme väärtusega kirjed olid tabelis viimased).

Indeksist otsimine kobarindeksist toimub analoogiliselt primaarvõtmega kahend-otsingu meetodil.

On võimalik ka selline lahendus, kus ühes plokis on ainult ühe võtme väärtusega kirjed ja kui nad sinna ära ei mahu, siis jätkuvad kirjed järgmises plokis. Iga uus võtme väärtus algab siiski uuest plokist. Ploki lõpus on viide järgmisele plokile, kus sama võtme väärtusega kirjed jätkuvad. See võimaldab muuta andme-tabelisse lisamist dünaamilisemalt. Indeksi kirje viitab alati ahela esimesele blokile (kust antud võtme väärtusega kirjed algavad). Sellise viitade süsteemi kasutusele võtmisel ei pea sama võtme väärtusega kirjeid sisaldavad leheküljed paiknema järjest, mis muudab oluliselt mugavamaks uute kirjete lisamise tabelisse - enam ei pea kirjetele" ruumi tegemiseks" suurema võtme väärtusega kirjeid "taha poole lükkama", et olemasolevate kirjete vahele "auku" teha:

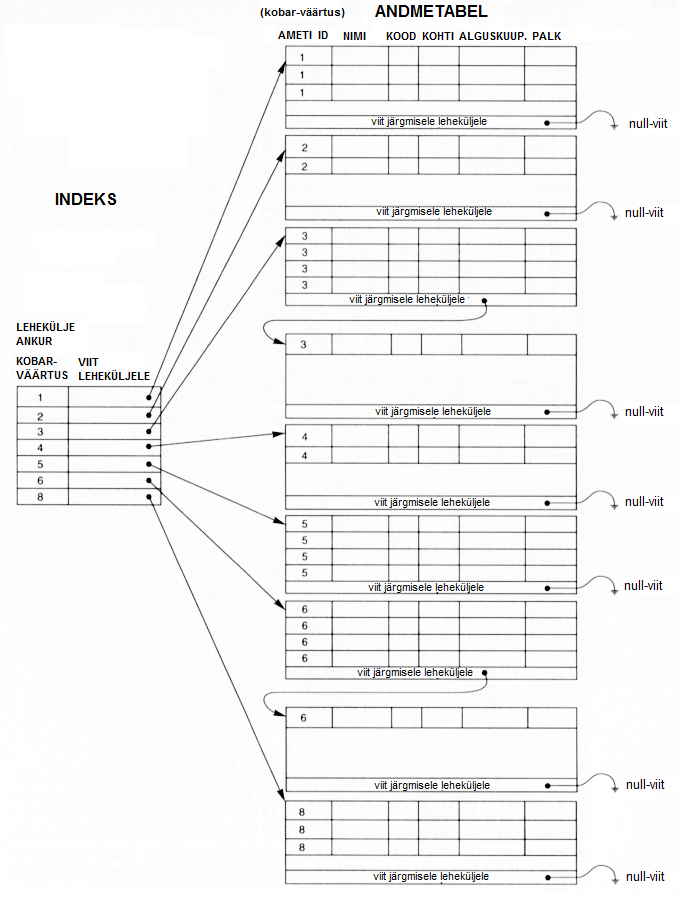
Siin on ikka lehekülje lõpus viit järgmisele leheküljele. Kui sama võtme väärtusega kirjed mahuvad ära samale leheküljele, siis on viida väärtus tühi (null viit). Kui sama võtme väärtusega kirjed jätkuvad järgmisel leheküljel, siis viitab lehekülje lõpus olev viit sellele leheküljele, kus sama võtme väärtustega kirjed jätkuvad.

Ka siin on mõned probleemid. Need tekkivad jällegi kirjete lisamisel, uuendamisel ja kustutamisel. Probleemi ei tekki kirjete sisestamisel andmetabelisse, kuna siin on võimalik vastavalt vajadustele lisada uusi lehekülg. Probleem tekkib aga indeksi kirjete lisamisel. Kuna indeks on tihe st. kõik võtme väärtused on indeksis ja ka järjestatud, siis tuleb iga uue võtme väärtuse tekkimisel andmetabelisse teha indeksisse "auk", selleks et uus indeksi võtme väärtus panna järjestuses õigesse kohta.

Kobarindeks on tihe, järjestatud ja ühe-tasemeline indeks. Tihe indeks, nagu ees poole kirjeldatud, tähendab seda, et kõigi andmetabeli kirjete võtmeväärtused on indeksis olemas. Järjestatud indeks tähendab seda, et indeksi kirjed on sorteeritud võtmeväärtuse kasvamise või kahanemise (sellel pole tähtsus kummas järjestuses) järjestuses. Ühe tasemeline indeks tähendab seda, et indeksi kõik kirjed paiknevad samal tasemel st. ühtses jadas.

14.2.1.3. Sekundaarindeks (Secondary Index)

Ka sekundaarse indeksi kirjetes on kaks veergu ja indeksi kirjed on järjestatud võtme väärtuse järgi. Samas on need väärtused andmetabelis unikaalsed (distinct). Seda väärtust nimetatakse mõni kord ka sekundaarseks võtmeks (secondary key) või alternatiiv-võtmeks (alternate key). Eelmistest indeksitest erinevalt ei ole indekseeritav väli andme-tabeli kirjete järjestamise aluseks – väärtused paiknevad andme-tabelis täiesti segamini.

Indeksi esimeses veerus on võtme väärtus, teises veerus viit leheküljele, kus kirje asub. Siin indeksis on kirje iga andme-tabeli kirje kohta – tegemist on tiheda (dense) indeksiga.

Kuna veerg, mille järgi indeks on koostatud ei ole andmetabeli kirjete sorteerimise aluseks, siis ei nimetata seda võtmeks vaid lihtsalt indekseerimisväärtuseks ja tabeli veergu, milles indekseerimisväärtuseks on, indekseeritud veeruks.

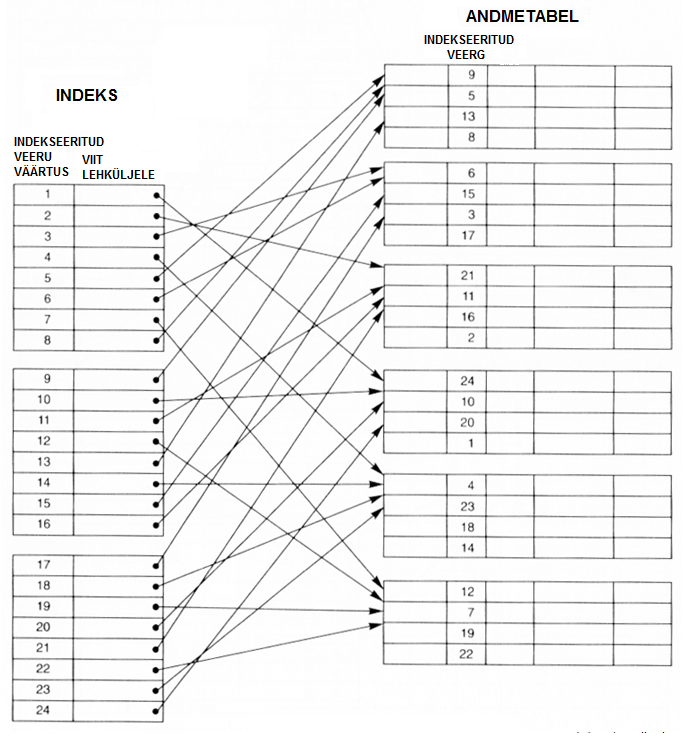
Sekundaarindeksit kasutatakse paralleelselt primaarindeksiga siis, kui tabelis on kaks veergude komplekti, mille väärtused on unikaalsed. Neist ühest tehakse primaarindeks ja selle järgi sorteeritakse tabeli kirjed. Teisest unikaalsest veergude komplektist tehakse sekundaarindeks. Tabelil võib olla rohkem kui üks sekundaarindeks. Sellisel juhul peab tabelis olema rohkem ka unikaalsete väärtustega väljade komplekte.

Sekundaarindeks on tihe, järjestatud ja ühe-tasemeline indeks. Tihe indeks tähendab seda, et kõigi andmetabeli kirjete võtmeväärtused on indeksis olemas. Järjestatud indeks tähendab seda, et indeksi kirjed on sorteeritud võtmeväärtuse kasvamise või kahanemise (sellel pole tähtsus kummas järjestuses) järjestuses. Ühe tasemeline indeks tähendab seda, et indeksi kõik kirjed paiknevad samal tasemel st. ühtses jadas.

14.2.2. Mitmetasemelised indeksid (Multilevel Index)

Ühe tasemelistest indeksitest otsimisel pidime me läbi tegema log₂n sammu, kus n on indeksi kirjete arv, et leida indeksist ette antud võtmega kirje ja saada teada lehekülje aadress, kus asub kirje või tõdeda, et sellise võtmega kirjet tabelis pole. See on tingitud sellest, et iga valikuga vähendame me läbi vaadatavate kirjete hulka kaks korda (kahend-otsing).

Mitmetasemeliste indeksite mõte on vähendada indeksi otsingu iga sammu järel läbi vaadatavate indeksi-kirjete hulka rohkem kui kaks korda. See tähendab, et kogu otsing koondub kiiremini.

Vaatleme näiteks kahe tasemelist indeksit, mis on ehitatud primaarse indeksi põhimõttel. Siin on indeksi esimene tase täpselt analoogiline ühetasemelise primaarse indeksiga. Nüüd aga jagatakse ka indeks plokkideks (lehekülgedeks) ja ehitatakse sinna peale teine indeksi tase, mis on primaarne indeks esimese taseme indeksile:

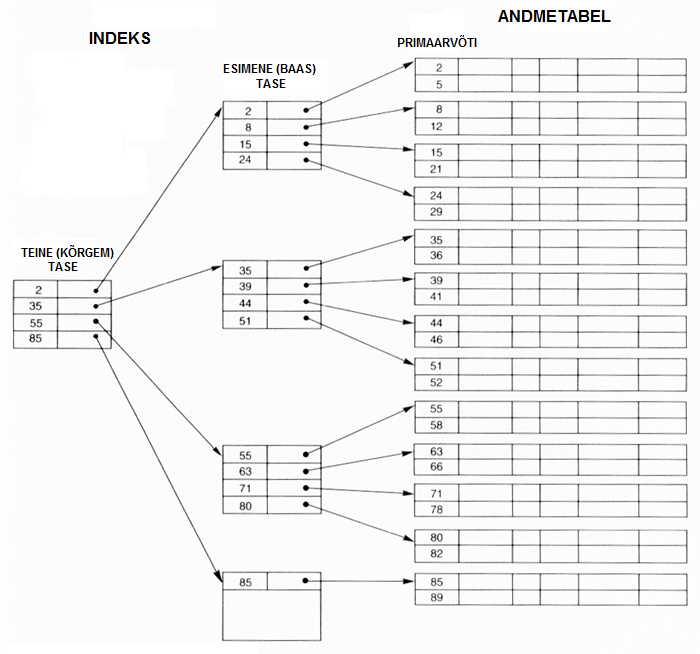
Kui siin indeksi esimese (baas) taseme bloki suuruseks on 10 indeksi kirjet ja kirjeid andmebaasis on 1 000 000 ja ka andmetabel on plokitud 10 kirje kaupa, siis indeksi esimesel tasemel on ligikaudu 100 000 kirjet ja indeksi teisel tasemel ligikaudu 10 000 kirjet. Esimene otsing sooritatakse teisel tasemel ja 10 000 kirje hulgas koondub otsing 14 korraga. Leitud aadressi järgi on vaja lugeda puhvrisse sisse esimese taseme indeksi blokk ning lugeda sealt selle lehekülje aadress andmetabelis, kus asub kirje ja seejärel lugeda leitud aadressi järgi sisse andmetabeli lehekülg. Seega kokku 16 lugemist. Sama protsess ühe-tasemelise indeksi korral oleks nõudnud 21 lugemist. See vahe tundub küll väike, aga miljonite otsingute läbiviimisel on kokkuhoid märkimisväärne. Kui lehekülgede pikkust suurendada väheneb kirje leidmiseks (või tõdemiseks, et sellise võtmeväärtusega kirjet baasis pole) kuluvate otsingupäringute arv.

Indeksi tasemeid ei pea olema sugugi ainult kaks, vaid neid võib olla oluliselt rohkem. Nendest tasemetest esimene on alati baastase ja viimane on kõrgeim tase.

Sama moodi võib tasemeteks jagada mistahes ees pool kirjeldatud ühe tasemelisi indekseid ja saada sedasi võitu otsingu kiiruse tõstmisel.

See mitme-tasemeline primaarindeks on hõre ja järjestatud.

14.3. Paisk-indeksid (Hash Index)

Ühe tasemelistest indeksitest otsimisel pidime me läbi tegema log₂n sammu, kus n on indeksi ridade arv, et leida indeksist ette antud võtmega kirje ja saada teada lehekülje aadress kus asub kirje. Mitme tasemelistes indeksites on otsingu koondumise kiiruseks suurem, log2(n/m*z)+z, kus m on indeksi tasemete arv ja z on kirjete arv indeksi leheküljel. Kuid ikkagi on mõnikord situatsioone kus päringu kiirus on nii oluline, et vaja oleks vähendada indeksi lugemiste arvu enamikel juhtudel ühe korrani, mitte aga rohkema kui kolme kuni nelja korrani.

Sellise lahenduse pakub meile paisk-indeks. Paisk-indeksi toimimine on kardinaalselt teistsugune kui meie poolt seni vaadeldud indeksitel. Vaatame, milles on erinevused. Teeme selleks võrdlustabeli:

Eelnevalt vaadeldud indeksid	Paisk-indeks
indeksil on kaks veergu: võtme väärtus ja viit andmetabeli leheküljele	indeksil on alati kolm veergu: võtme väärtus, viit andmetabeli leheküljele ja viit kollisiooni ahela järgmisele kirjele
indeksi kirjed on järjestatud võtmeväärtuse järgi	indeksi väärtused on indeksis paisatud näiliselt juhuslikult, tegelikult arvutatakse indeksi väärtuste asukoht (kirje järjenumber) indeksiga seotud valemi alusel
indeksi ridade arvu suurendatakse/vähendatakse vastavalt sellele, kuidas andmetabelis ridade arv suureneb ja väheneb	indeks tehakse tema loomisel valmis tema maksimaalse võimaliku ridade arvuga.: indeks täidetakse tühjade ridadega. Kui indeksi ridade arvu on vaja muuta (tavaliselt suurendada) tuleb indeks luua uuesti, sedakorda siis juba suurema või väiksema ridade arvuga. Paisk-indeksi ridade arv peaks olema umbes 20% suurem, kui on seda maksimaalselt andmetabelisse lisatavate kirjete arv.
võtme indeksist leidmiseks kuluv lugemiste arv sõltub indeksi ridade arvust ja on seda suurem, mida rohkem on indeksis (seega ka andmetabelis) ridu	võtme indeksist leidmiseks kuluv lugemiste arv ei sõltu indeksi ridade arvust vaid sellest, kui õigesti on arvutatud paisk-indeksi ridade arv; suurem ridade arv annab tavaliselt paremaid tulemusi.

Kuidas töötab siis see esmapilgul oma omaduste poolest "müstilisena" tunduv konstruktsioon? Aga hakkame otsast pihta.

Võtame paisk-indeksi kolm omadust, mis võimaldavad meil teha temast "passipildi" - paisk-indeksil on kolm veergu paisk-indeksil on alati fikseeritud arv ridu ja paisk-indeksi ridade arv peaks olema ca 20% suurem, kui on maksimaalselt võimalik lisada kirjeid andmetabelisse, mille jaoks on see paisk-indeks loodud:

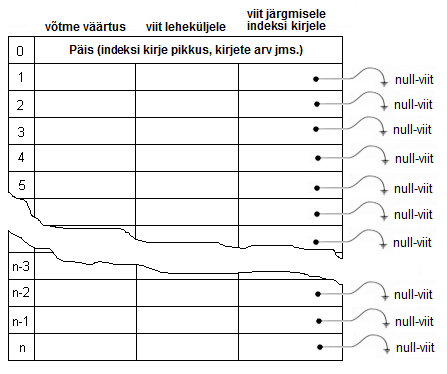
Siin indeksi ridade väärtus n saadakse andmetabeli maksimaalsest kirjete arvust m: n=1,2*m. Selline paisk-indeksi tabeli ridade arvu kalkulatsioon ei ole mingil määral kohustuslik ja soovituslik koefitsiendi suurus erinevate andmebaasisüsteemide puhul võib olla erinev. See koefitsient on siin võetud ainult näite koostamiseks. Tühjas tabelis kirjutatakse kõikide ridade järgmise kirje viida väärtuseks null-viit (tühi viit).

Tabel on meil valmis, kuidas satuvad siia tabelisse nüüd indeksi kirjed? Iga paisk-indeksi tabeliga on seotud funktsioon x=f(y), kus y on võtme väärtus ja x on selle võtme väärtuse all kalkuleeritud rea number, kuhu võtme väärtus y koos lehekülje aadressiga kirjutatakse. Funktsiooni f nimetatakse paisk-funktsiooniks. Ja tegevust, kus paisk-funktsiooni järgi võtme väärtuse alusel arvutatakse indeksi kirje rea aadress, kuhu see võtme väärtus koos lehekülje viidaga kirjutatakse, nimetatakse paiskamiseks.

Andku meie võtme väärtus "Kai Mai' funktsioonil f tulemuse 3. See tähendab seda, et võtme väärtus "Kai Mai' tuleb paigutada paisk-indeksi kolmandasse ritta:

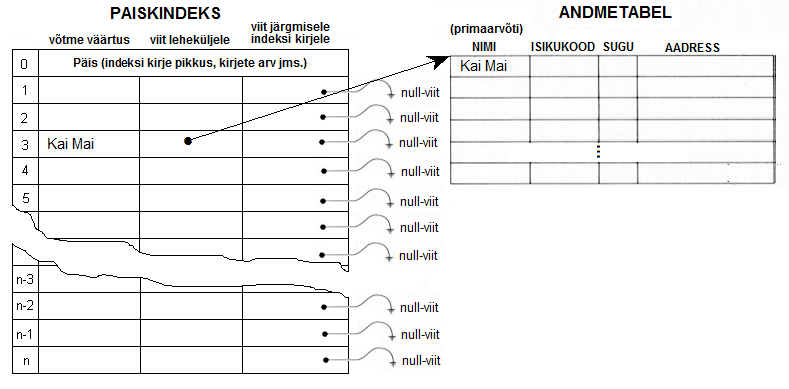
Andmetabelisse lisati esimesele leheküljele esimene kirje. Paisk-indeksi kolmandale reale kirjutatud võtmeväärtus viidatakse andmetabelisse kirjutatud kirjele. Kui me nüüd tahame teada, kas mingi võtme väärtusega kirje on andmetabelis olemas peame me võtma sama funktsiooni, millega me "paiskasime" võtme väärtuse indeksisse, arvutama otsitavale reale indeksi rea numbri ja vaatama, kas indeksi selle rea peal on sellise väärtusega võtme väärtus.

Püüame näiteks mõelda, kuidas kirjutada algoritm, mis enne uue isiku andmete andmetabelisse lisamist kontrolliks, kas sellise nimega isiku andmed on juba tabelis olemas. Kui on, siis ei lisata, kui ei ole, siis lisatakse andmetabelisse uue isiku andmed:

1. Olgu meil selle inimese nimeks, kellel andmeid me andmetabelisse kirjutada tahame, "Vello Põlu"
2. Arvutame võtme väärtusele "Vello Põllu" funktsiooniga f, selle indeksi rea numbri, kus võti "Vello Põllu" peaks olema. Oletame et f("Vello Põllu") tulemuseks on 4.
3. Kontrollime, milline väärtus on paisk-indeksi real 4; saame teada, et sealne väärtus on tühi ja järelikult pole "Vello Põllu" nimelist isikut andmetabelis olemas ja me võime ta sinna lisada

Selle tulemusena on seis andmetabelis ja indeksis järgmine:

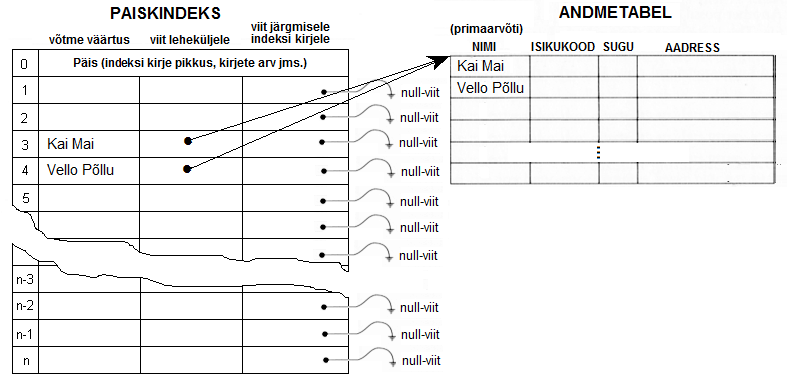
Kõik tundub täiesti selge olevat, kui poleks ühte pisikest nüanssi - vahel võib funktsiooni x=f(y) tulemus erinevate võtme väärtuste y1 ja y2 puhul anda sama indeksi rea numbri x. Kui kõigepealt kirjutada tabelisse võtme väärtus Y1 on kõik korra, sest indeksi rida on positsioonis x tühi. Kui nüüd aga hakata salvestama võtme väärtust y2, siis oleme probleemi ees - indeksi rida, kuhu võtme väärtust y2 soovitakse kirjutada, on juba võtme väärtus y1 ees.

Sellistel juhtudel käitutakse nii, et uue väärtuse jaoks valitakse mingi teine vaba rida indeksi tabelis. Selle valimiseks kasutavad erinevad andmebaasisüsteemid erinevaid meetodeid aga ei ole vale mõelda, et selleks reaks võetakse esimene järgnev tühi rida.

Teeme siis oma näidet edasi. Oletame, et tabelisse soovitakse lisada isikut kelle nimi on "Kati Mati". Funktsioon f annab "Kati Mati" jaoks indeksi rea 3. Kontrollimisel selgub, et see rida on juba täidetud aga see kelle andmed sinna kirjutatud on pole sugugi "Kati Mati". Seega "Kati Matit" baasis pole. Andmebaasisüsteem paigutab "Kati Mati" andmed indeksis reaale 5 (esimene järgnev vaba rida indeksis) ja viitab rea 3 (selle rea, kuhu "Kati Mati" väärtus pidi funktsiooni f tulemuse alusel tegelikult kirjutatama) järgmise kirje viida sellel kirjele, kuhu "Kati Mati" indeksi võti tegelikult kirjutati:

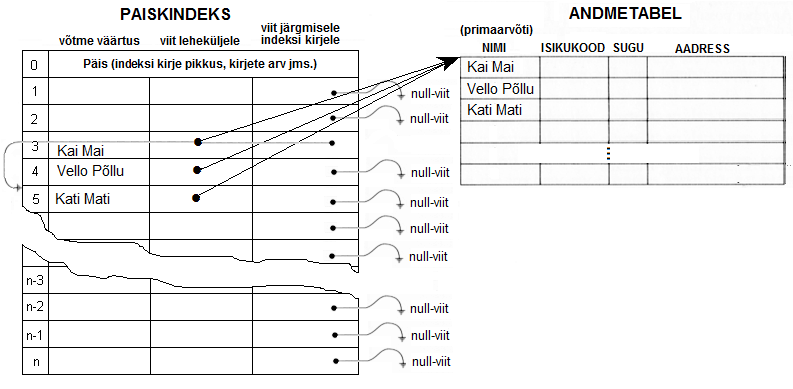
Kuidas toimub sellises indeksis võtme "Kati Mati" otsimine? Kõigepealt arvutatakse funktsiooni f järgi välja võtme "Kati Mati" rea number indeksis. Sealt realt kontrollimisel selgub, et selle kirje võtme väärtus "Kati Mati" küll pole. Samas näeme aga, et järgmise kirje viida väli pole tühi. Nüüd loetakse järgmise kirje viida väärtus ja vaadatakse, ega võtme väärtus "Kati Mati" pole ehk selles reas. Ja loomulikult leitaksegi see väärtus sealt.

Sellist ahelat, mis tekkib indeksi nendest kirjetest, mida funktsioon määrab sama indeksi rea peale kirjutatavateks nimetatakse kollisiooni ahelaks. Tegelikkuses võib kollisiooni ahel olla kui tahes pikk aga sellisel juhul kaotab paisk-indeks oma efektiivsuse. Seepärast tehaksegi paisk-indeksi tabelitesse rohkem ridu, kui on maksimaalselt võimalik nendes andmetabelites mida nad indekseerivad - suurema arvu kirjete peal hajub "paiskamine" paremini. Seega, kui paisk-indeksis lähevad kollisiooni ahelad liiga pikaks, tuleb indeks hävitada ja luua suurema ridade arvuga uuesti.

Kui paisk-indeksi kõik read on täidetud, siis ei saa andmetabelisse enam ühtegi kirjet lisada, kuna indeksisse ei õnnestu lisada enam ühtegi uut väärtust. Sellist situatsiooni ei tohi andmebaasis lasta tekkida. Juba siis kui selline "oht paistab kauguses" tuleb paisk-indeks hävitada ja luua see uuesti ja siis juba suurema ridade arvuga.

Vaatame nüüd näidet edasi. Kuidas saab kollisiooni ahelas kontrollida, et otsitavat võtme väärtust ahelas pole. Oletame, et võtme väärtus "Kaja Maja" annab jällegi funktsioonil f tulemuseks rea numbri 3. Kontrollime võtmeväärtust "Kaja Maja" vastu indeksi kolmandat rida. Saame tulemuseks, et kontrollitav väärtus ei lange real oleva väärtusega kokku. Leiame viida järgmisele reale ja kontrollime otsitavat väärtust nüüd selle rea vastu uuesti. Saame jälle negatiivse tulemuse. Kuna selle rea peal enam viita järgmisele reale pole (seal on null-viit), siis loeme otsingu lõppenuks ja tõdeme, et võtme väärtust "Kaja Maja" indeksis pole ja seega pole sellise võtme väärtusega kirjet ka andmetabelis.

Paisk-indeksi suurimaks miinuseks on see, et ta tuleb kohe alguses täies mahus valmis ehitada ja seepärast reserveerib see kohe (olenemata andmetabeli suurusest) täies mahus ketta ruumi. Seepärast kasutatakse neid harva. Teisest küljest vaadatuna ei ole üldse väga palju kohti kus neid kasutada tasuks.

Paisk-indeksid on tihedad, järjestamata ja mitme tasemelised. Paisk-indeksite mitmetasemelisus kujuneb dünaamiliselt läbi kollisiooni ahelate. Kuna paistabelis paiknevad võtmeväärtused "kaootiliselt segamini", siis on tegemist järjestamata indeksiga. Paisk-indeksis on andmetabeli kõigi unikaalsete võtmete väärtused. Seega on paisk-indeks tihe.